An Introdution To Random Forests: The Theory

It’s been a while since I’ve blogged, especially about anything computer science related, so here goes.

This is going to be a two part introduction to the machine learning technique/framework called Random Forests. Random forests the have gained much popularity in recent years owing to it’s ability to handle extremely large training data efficiently as well as provide O(n) test time efficiency.

Before we can talk about random forests we must understand decision trees, and decision tree learning. I feel that it’s much easier to learn through example, so I will go through a simple one from the book: Machine Learning by Tom Mitchell.

The goal is to be able to predict whether or not to play tennis on a Saturday morning given the following attributes $\{weatheroutlook, temperature, humidity, wind\}$. In this example we will be performing supervised learning, which is where we are given labelled training data. Going back to our example, the labelled training would look something like this:

Note:The labels are the playTennis column (yes,no).

Data ID	Weather Condition	Temperature	Humidity	Wind	PlayTennis
d1	Sunny	Hot	High	Weak	No
d2	Sunny	Hot	Normal	Strong	Yes
d3	Rain	Mild	Normal	Weak	No

From this data we wish to build a decision tree which, such that for an input $x=\{weatheroutlook, temperature, humidity, wind\}$ we can follow a path to a leaf node which contains the answer $yes,no$.

In order for us to reach the correct leaf node, at each non-leaf node (called split nodes), a function $g(x)$ is evaluated on the input and based on the result we branch either right or left until we reach a leaf node which will contain the result (to play tennis or not).

The question now is, what qualities should the functions $g(x)$ have and how do we generate a good function, $g(x)$, using the training data?

Well, Ideally we would just have one split node which would contain a test function that managed to split the training data into two sets, $S_i$ and $S_j$, such that all members $x_i \in S_i$ have attribute $playTennis = No$ and $x_j \in S_j$ have attribute $playTennis = Yes$.

This situation may arise in very simple problems, or training data that doesn’t fully represent the problem. For example, look at the graph below, it shows that the data points can easily be split into two classes by the simple function $f(x) = x>5$. However, in real life situations data is seldom separated this easily, in fact real data is rarely linearly separable and can possibly only be split by a high dimensional hyperplane represented by a very complex function. It is, in fact, the combination of the simple split node tests, that together form a highly non-linear separation of the data in to the desired classes.

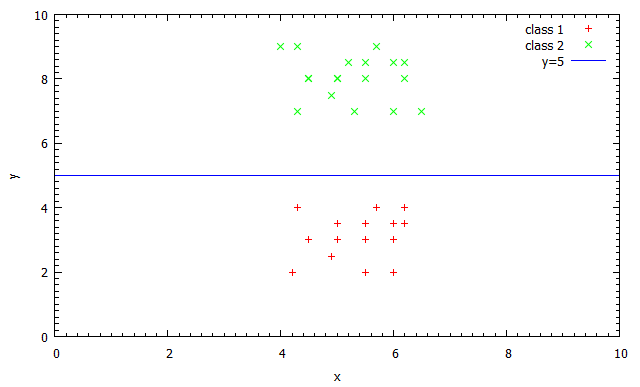
An example of linearly seperable data.

An example of linearly seperable data.

Even though it is unlikely that just one split function will be able to partition the data perfectly, I hope it has become clear that we would like a split function that maximizes this separation. In fact, we wish to maximize the information gain at each split node. The information gain of the function at a split node is a measure of much the function decreases the uncertainty of the class label in the data. For example, given data $\{a,a,a,a,b,b,b\}$ , a split function that splits the data into $\{b,b,b\} \& \{a,a,a,a\}$ would have a higher information gain than one that splits it into $\{a,a,b,b\} \& \{a,a,b\}$ as clearly the uncertainty of class label is lower in the sets produced by the first split than the second.

More formally, information gain is defined as the change in entropy ($H$) from a prior state (the training data at the node, $S$) to a new state (the subsets generated, $S_i$). This is denoted by the following formula (in this case we are using the Shannon Entropy as our measure):

note: $C$ is the set of all classes, in our example this is $\{yes,no\}$.

$$ IG(S) = H(S) - \sum\limits_{i} w_i \times H(S_i) \\where: \\H(S) = - \sum\limits_{c \in C}{P(c|S) \times log_2(P(c|S))}\\w_i = \frac{|S_i|}{|S|} $$

So, at each node we wish to choose the function that maximizes the information gain. Now, returning to decision tree learning, the following algorithm, called C4.5, is used to grow our tree:

If we should terminate, create leaf node. Else
For each attribute a
Find the normalized information gain from splitting on a
Let a_best be the attribute with the highest information gain
Create a decision node that splits on a_best
Recurse on the subsets obtained by splitting on a_best, and add those nodes as children of the current node

Returning to our example, for our terminating criterion we will stop if all data samples at the node have the same class, which is all yes or all no in our case. So given the training data, we start at the root of the tree and check, for each attribute, the information gain. For example, given the 3 data examples at the top, using the attribute $wind$ , we calculate the information gain as follows:

First, we calculate the entropy, $H(S)$ , of the whole set $S=\{d1,d2,d3\}$ as follows:

$$ H(S) = - \sum\limits_{c\in\{yes,no\}}P(c|S) \times log_2\left(P\left(c|S\right)\right) $$ $$ H(S) = -\left(\frac{1}{3} \times log_2\left(\frac{1}{3}\right) + \frac{2}{3} \times log_2\left(\frac{2}{3}\right)\right) $$ $$ H(S) = 0.91829583405 $$

Split the data into two sets based on the possible values the attribute $wind$ can take ($\{weak,strong\}$). This produces the following sets $S_1 = \{d1,d3\} \& S_2 = \{d2\}$ , where $S_1$ has $wind = weak$ and $S_2$ has $wind = strong$.

$$ H(S_1) = -\left(0 + \frac{2}{2} \times log_2\left(\frac{2}{2}\right)\right) = 0 $$

and $w_1 = \frac{2}{3}$ as $S_1$ contains two of the three training datum.

$$ H(S_2) = -\left(\frac{1}{1} \times log_2\left(\frac{1}{1}\right)\right) = 0 $$

and $w_2 = \frac{1}{3}$.

So the information gain ($IG$) is:

$$ IG(S) = H(S) -\sum\limits_{i=\{1,2\}}w_i \times H(S_i)\\ IG(S) = 0.91829583405 - (0 + 0) = 0.91829583405 $$

Similarly, we check for the attributes $weathercondition$, $temperature$ and $humidity$, which give us information gains of $-0.08170416595$, $-0.08170416595$ and $-0.08170416595$ respectively. As we are trying to maximize information gain, we choose wind as the best attribute and split the data on this attribute.

We now recurse on the two subsets produced ($S_1$ & $S_2$ as above), which we can see both contain data from just one class which matches our termination criterion. So, we have now how two leaf nodes, and have built our tree.

Given our tree, given a new input $x$, we check the $wind$ attribute and if it is $weak$ we answer $no$ else if it is $strong$ we answer $yes$. Obviously this was highly simplified by the fact that we only used 3 training samples, which is hardly enough to capture the problem accurately. Nevertheless, I hope this example has made the algorithm clear.

In the second part of this post I will discuss the down side of using this approach and why we use random trees. Additionally (hopefully) I will have a walk through, with code, of a real application using random forests. The application will probably be some form of image classification, such as classifying images as either images of cats or dogs, or if I have the time perhaps I can try and tackle a where’s Wally solver.

Alykhan Tejani

An Introdution To Random Forests: The Theory

You might also enjoy (View all posts)